设置
结果 (当前金币: 0)
| 金额 | 最少硬币数 | 最优组合 | 状态转移过程 |
|---|
什么是动态规划?
动态规划是一种通过把原问题分解为相对简单的子问题来求解复杂问题的方法。它的核心思想是:
- 将复杂问题分解成相互关联的子问题
- 通过解决子问题来解决原问题
- 保存已解决的子问题结果,避免重复计算
能用动态规划思路解决的问题一般有下面的特点:
- 最优子结构:问题的最优解包含子问题的最优解;
- 重叠子问题:在求解过程中,相同的子问题会重复出现;
- 状态转移:找到子问题之间的关系,通过状态转移方程来解决问题。
解决动态规划问题时,我们需要按照以下步骤系统地思考和解决:
- 定义状态:首先要思考如何用数学语言描述问题。定义状态是整个解题过程中最关键的一步,它决定了我们如何存储和使用计算结果。我们需要仔细思考:要解决的问题需要哪些变量来表示?这些状态通常会以数组的形式存储下来。一个好的状态定义应该能够完整地描述问题在某个阶段的情况。
- 找出状态转移方程:当我们定义好状态后,需要思考状态之间是如何转移的。也就是说,如何从已知的状态推导出新的状态,状态转移方程是解决问题的核心,一般想明白状态转移方程问题就解决了。
- 确定初始状态和边界条件:有了状态转移方程后,我们需要确定问题的初始状态。同时,我们还需要考虑一些特殊情况,比如输入为0或负数时应该如何处理。
- 按照状态转移方程求解:最后一步是实际求解过程。我们通常会按照一定的顺序(比如从小到大)来计算每个状态的值。在这个过程中,我们使用已经计算出的状态值,通过状态转移方程来得到新的状态值。这个过程需要特别注意计算的顺序,确保在计算某个状态时,它依赖的所有状态都已经计算出来了。
动态规划硬币找零问题
下面结合生活中常见的一个场景来理解动态规划。
硬币找零问题来自生活中的一个常见场景。给定一组不同面值的硬币,然后给定一个目标金额。我们的目标是计算出凑到目标金额所需的最少硬币数量。
首先思考我们需要求解的是"凑出某个金额所需的最少硬币数"。那么我们可以定义状态 dp[i] 表示:凑出金额 i 所需的最少硬币数量。
现在思考:如何从已知状态推导出新状态?
假设我们要计算 dp[i],也就是凑出金额 i 所需的最少硬币数,那么可以拆分为下面的子问题:
- 如果我们选择使用了某个面值 m 的硬币,那么问题就转化为:凑出金额 (i-m) 所需的最少硬币数,再加上这一个新使用的硬币;
- 由于我们要求的是最少硬币数,所以需要在所有可能的硬币选择中取最小值;
因此,状态转移方程如下,其中 m 遍历所有可用的硬币面值:
dp[i] = min(dp[i-m] + 1)
然后需要确定初始状态和边界条件:
- 当金额为 0 时,不需要任何硬币,所以 dp[0] = 0;
- 对于其他金额,初始时设为无穷大,表示还未找到凑出该金额的方案;
- 在计算某个状态时,只有当 i ≥ m 时才能使用面值为 m 的硬币。
接着我们结合本页面的可视化工具,来直观感受下动态规划的求解过程吧。
动态规划可视化工具说明
本页面的可视化工具分为左右两个主要区域,在右侧的设置面板中,你可以自定义问题的参数。
首先,你可以设置想要凑出的目标金额,系统默认设置为11。接着,你可以通过添加或删除不同的硬币面值来调整可用的硬币种类,默认提供了面值为1、2、5的三种硬币。设置完这些参数后,你就可以通过控制按钮来观察求解过程。
控制按钮提供了两种执行方式:如果你想要详细了解每一步的计算过程,可以选择"逐步执行"模式,这种模式下系统会在每一步计算时暂停,让你能够清楚地观察状态是如何转移的。如果你只关心最终结果,可以选择"快速完成"模式,系统会直接展示完整的解决方案。
在左侧的结果显示区域,你会看到一个动态更新的表格。这个表格会展示从0到目标金额的每个金额的求解情况。对于每个金额,你都能看到三个关键信息:凑出该金额需要的最少硬币数量、具体使用了哪些硬币(最优组合),以及是如何从之前的状态转移得到当前解的。
为了让计算过程更加直观,系统使用了不同的颜色标记来突出显示重要信息。当前正在计算的步骤会用黄色高亮显示,这样你能够清楚地跟踪计算的进度。当发现了更优的解法时,相关的状态转移路径会用绿色标记出来。同时,系统还会用图形化的方式展示硬币的组合,让你能够直观地看到每个金额的最优解是如何由硬币组合而成的。
让我们看一个具体的例子。当我们设置目标金额为11,使用面值为1、2、5的硬币时,系统会逐步展示计算过程。如下图:
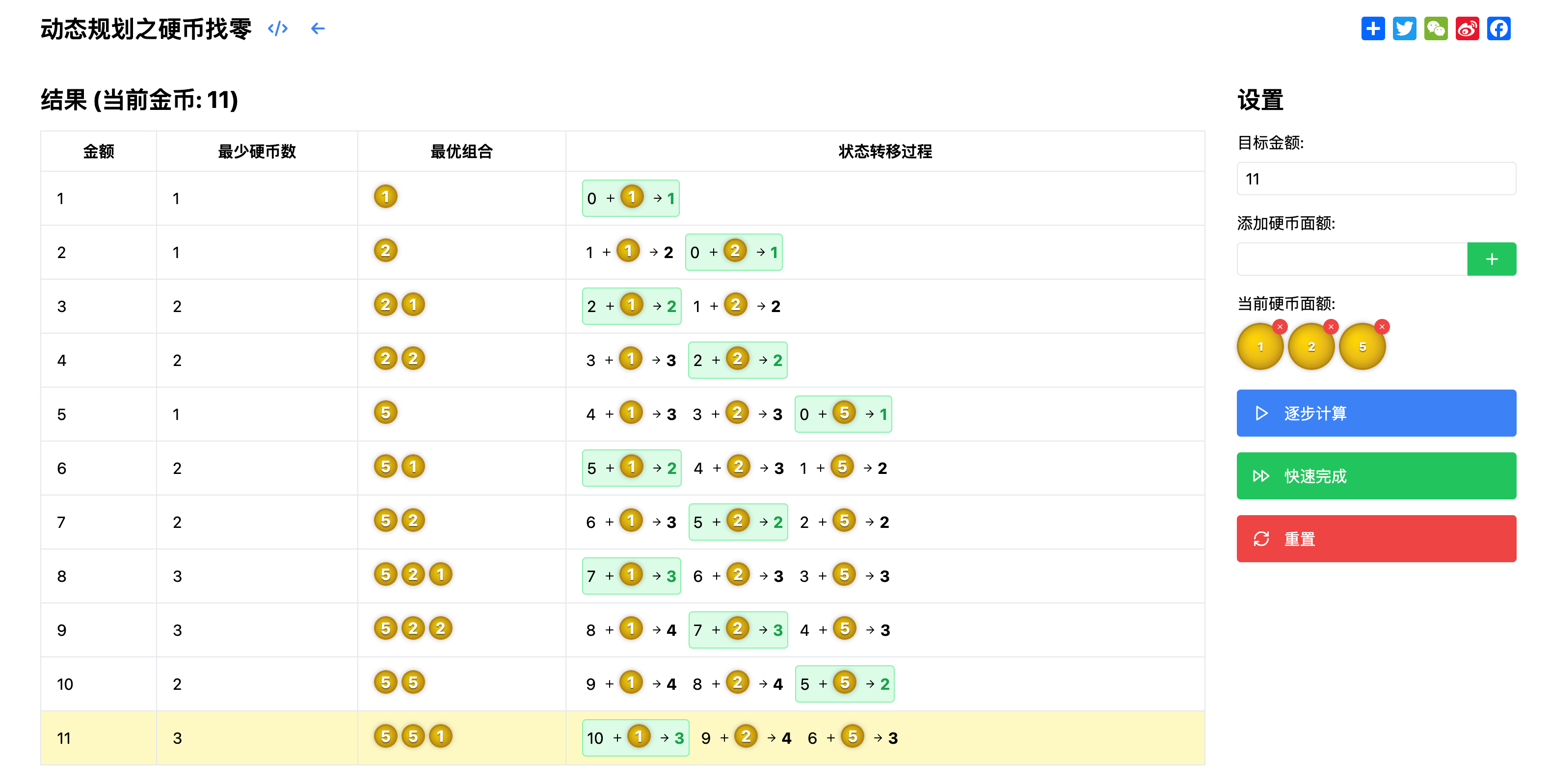
每个金额的最优解计算过程:
- dp[1] = min(dp[1-1] + 1) = dp[0] + 1 = 1
- dp[2] = min(dp[2-1] + 1, dp[2-2] + 1) = min(2, 1) = 1
- dp[3] = min(dp[3-1] + 1, dp[3-2] + 1) = min(2, 2) = 2
- dp[4] = min(dp[4-1] + 1, dp[4-2] + 1) = min(3, 2) = 2
- dp[5] = min(dp[5-1] + 1, dp[5-2] + 1, dp[5-5] + 1) = min(3, 3, 1) = 1
...以此类推。通过这种可视化的方式,你可以清晰地理解动态规划的求解过程,看到状态是如何一步步转移的,以及最优解是如何被找到的。这对于理解动态规划的核心思想和解题思路都很有帮助。
动态规划的难点
动态规划虽然是一个强大的解题工具,但在实际应用中往往会遇到以下几个主要难点:
定义一个好的状态:最具挑战性的往往是找到合适的状态定义。一个好的状态定义需要满足两个关键要求:既要能完整描述问题,又要尽可能简单。有时候看似合理的状态定义,可能会导致无法推导出状态转移方程,这时就需要重新思考状态的定义方式。
状态转移方程的推导:即使正确定义了状态,找到状态之间的转移关系依然很困难。我们需要思考:当前状态和哪些之前的状态有关?如何从这些状态推导出当前状态?有时候可能需要考虑多个维度的状态转移,这就大大增加了复杂度。
考虑下面的经典动态规划问题,看你能不能想到合适的状态定义和状态转移方程。
- 编辑距离问题:给定两个字符串,计算将一个字符串转换成另一个所需的最少操作次数(可以插入、删除、替换字符)。
- 最长子序列和问题:给定一个整数数组,找出其中和最大的连续子序列。
- 背包问题:给定一组物品,每个物品有重量和价值,在限定的总重量内,如何选择物品使得总价值最大。
面对比较难的题目,可以尝试下面的思路,看能不能用动态规划解决。
- 从最简单的例子开始,手动推演几个小规模的情况;
- 尝试不同的状态定义,直到找到能够表达完整问题的定义;
- 画图辅助思考,特别是对于需要考虑区间或多维状态的问题;
- 多关注状态之间的转换过程,而不是具体的数值;
- 验证特殊情况下的正确性,比如输入为空或只有一个元素时的情况。